分光分布曲線とは？

前稿に引き続き、分光分布について解説していく。

分光分布曲線を描く

前稿では$680\,\mathrm{nm}$から$730\,\mathrm{nm}$までの赤色波長域に含まれる放射束を計測し、それを波長域の長さ$50\,\mathrm{nm}$で割った放射束密度を求め、横軸に波長・縦軸に放射束密度をとったグラフを描いた▼

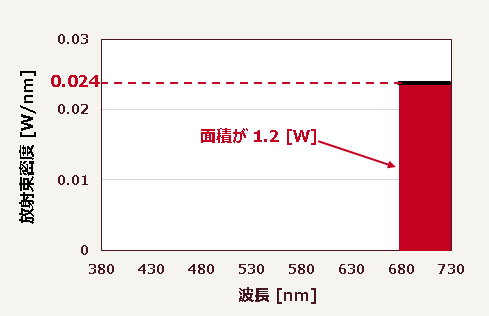
同じ操作を、他の波長域、すなわち黄・緑・青・藍・紫の光についても同様に行い、このような結果になったとする▼

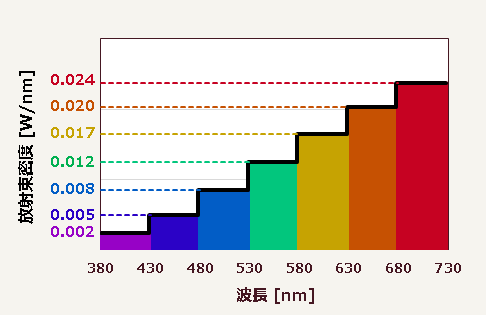
このグラフは$50\,\mathrm{nm}$という長さの波長域ごとに放射束密度を調べた結果だ。これを分光分布と言っても間違いではないのだが、若干の問題がある。問題とは精度の話で、要するに波長域が長すぎる（波長分解が粗すぎる）。もっと短い波長域で検討する必要があるのだ。そこで、波長域を$40\,\mathrm{nm}$として全く同じ作業をすると、このようになる▼

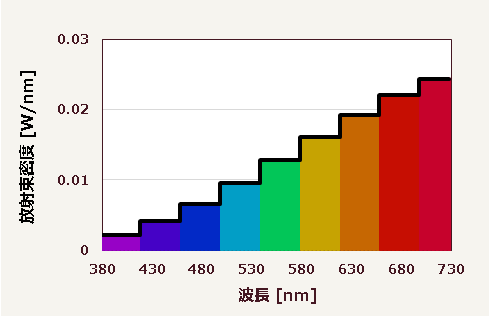
波長域を$20\,\mathrm{nm}$とすると、このようになる▼

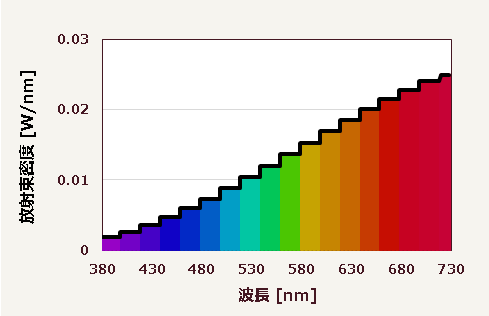
このように、注目する波長域を極限まで短くしていった結果、グラフは次第に曲線を描くようになる。波長域$2\,\mathrm{nm}$でこのようになる▼

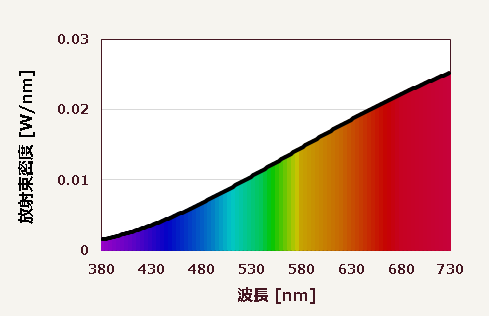
これがいわゆる分光分布曲線である。曲線に見えるだけで、実際は踏面長$2\,\mathrm{nm}$の階段状のグラフである。ちなみに分光分布は正確に言うと放射量の分光密度分布となるのであろうが、普通は単に分光分布という。

放射束を放射束密度で表現する

波長域が広い場合

再びこのグラフを登場させる。

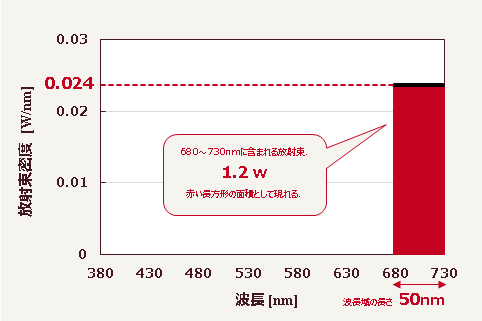
$680\,\mathrm{nm}$から$730\,\mathrm{nm}$までの赤色波長域に含まれる放射束$1.2\,\mathrm{W}$を計測し、それを波長域の長さ$50\,\mathrm{nm}$で割った放射束密度$0.024\mathrm{W/nm}$を求め、横軸に波長・縦軸に放射束密度をとったグラフだ。

放射束密度$0.024\,\mathrm{W/nm}$を得る計算過程はこのとおり▼

$0.024\,\mathrm{W/nm}=1.2\,\mathrm{W}/(730\,\mathrm{W}-680\,\mathrm{W})$

日本語で示すとこうなる▼

前稿の復習である。別段、難しい点はないと思う。

波長域が十分に狭い場合

では次に、注目する波長域を狭くすることを考える。

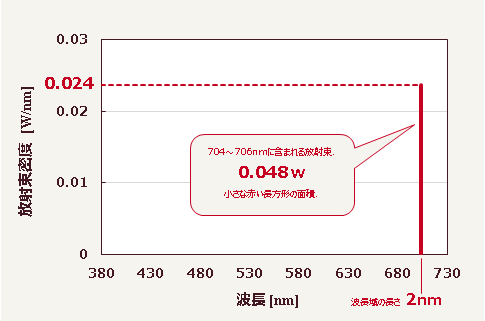
$704\,\mathrm{nm}$から$706\,\mathrm{nm}$までの波長域に含まれる放射束が$0.048\,\mathrm{W}$であった、という状況を示すグラフだ。このとき、放射束密度はこのように計算される▼

$0.024\,\mathrm{W/nm}=0.048\,\mathrm{W}/(706\,\mathrm{W}-704\,\mathrm{W})$

ここまでは波長域長さ$50\,\mathrm{nm}$の場合と変わらない。

ではこれを日本語で表現する。$0.048\,\mathrm{W}$というのは、$704\,\mathrm{nm}$から$706\,\mathrm{nm}$までの波長域に含まれる放射束である。これは正確な表現ではあるが、もはや波長域の長さがたったの$2\,\mathrm{nm}$であるから、$704$と$706$の中央値をとって、「波長$705\,\mathrm{nm}$の放射束は$0.048\,\mathrm{W}$」と言ってもいい気がしてこないだろうか。放射束密度も同様だ。つまりこういうことである▼

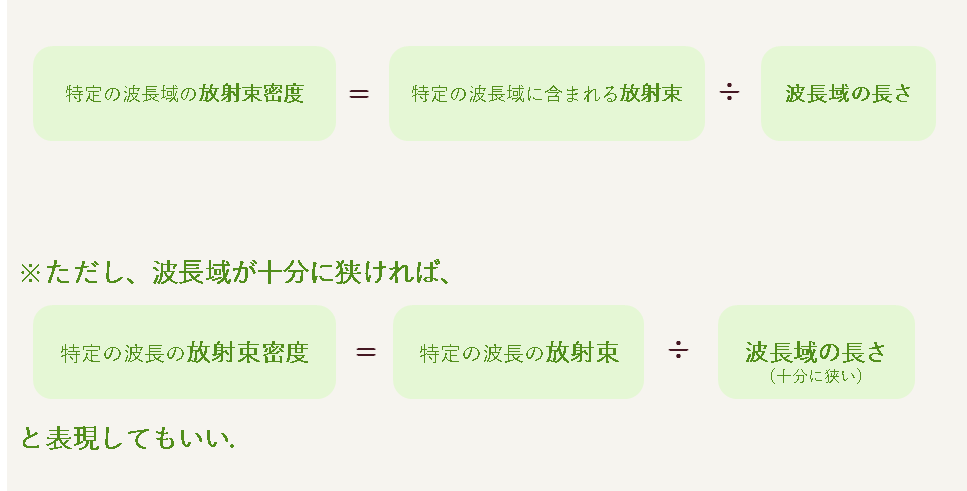
「波長域」という表現がなくなった。日本語の違いだけではないかと思われるかもしれないが、もう少しお付き合い頂きたい。

上の式を放射束について解いてみるとこのようになる▼

これが重要だ。本来、ある特定の波長の放射束というモノは直接計測ができない。しかし、放射束密度という考え方を取り入れることで、ある特定の波長の放射束を間接的に表現できる。ただし条件があって、波長域は十分に狭い必要がある、とうわけだ。

数式で表現してみよう。それぞれの値を下記のように表現することとする▼

　ある特定の波長$\lambda$の放射束：$\it\Phi_{\rm e}\rm(\lambda\rm)$
　ある特定の波長$\lambda$の放射束密度：$\it P\rm(\lambda\rm)$
　十分に狭い波長域の長さ：$\it\Delta\lambda$

これらを使うと、放射束はこのようになる▼

$\it\Phi_{\rm e}\rm(\lambda\rm)=\it P\rm(\lambda\rm)\it\Delta\lambda$

このように、ある特定の波長の放射束は、その波長における放射束密度が分かっていれば求めることができる。とういよりも、放射束は放射束密度を使わなければ表現できないのだ（レーザー光線などの特殊な光源は除く）。

ちなみに「十分な狭さの波長域」というのは感覚的な話ではなく、きちんとした検討の結果、およそ$2～5\,\mathrm{nm}$とされている。

分光分布から放射束を求める

本稿のまとめとして、分光分布という情報から放射束を求めてみよう。

まず、使う式は先ほどつくったこちら▼

$\it\Phi_{\rm e}\rm(\lambda\rm)=\it P\rm(\lambda\rm)\it\Delta\lambda$

そして、分光分布はこちらを使う▼

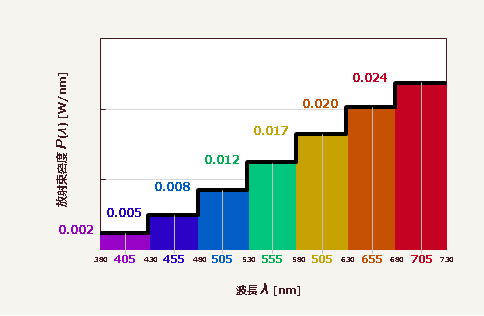
筆者が適当に作ったグラフであるが、一応、白熱電球の分光分布を模している。一番左、紫の部分は、波長$405\,\mathrm{nm}$を中心に$50\,\mathrm{nm}$の波長域を設定していて、その波長域での放射束密度は$0.002\,\mathrm{W/nm}$となっている。つまり、

　$\it P\rm(405)=0.002\,\mathrm{W/nm}$
　$\it\Delta\lambda=\rm 50\,\mathrm{nm}$

となるから、波長$405\,\lambda$の放射束は、

$\it\Phi_{\rm e}\rm(405)=\it P\rm(405)・\it\Delta\lambda=\rm0.002\,\times50=0.10\,\mathrm{W}$

と求めることができる。同様の操作を、全ての波長にわたって行う▼

$\it\Phi_{\rm e}\rm(455)=\it P\rm(455)・\it\Delta\lambda=\rm0.005\,\times50=0.25\,\mathrm{W}$
$\it\Phi_{\rm e}\rm(505)=\it P\rm(505)・\it\Delta\lambda=\rm0.008\,\times50=0.40\,\mathrm{W}$
$\it\Phi_{\rm e}\rm(555)=\it P\rm(555)・\it\Delta\lambda=\rm0.012\,\times50=0.60\,\mathrm{W}$
$\it\Phi_{\rm e}\rm(605)=\it P\rm(605)・\it\Delta\lambda=\rm0.017\,\times50=0.85\,\mathrm{W}$
$\it\Phi_{\rm e}\rm(655)=\it P\rm(655)・\it\Delta\lambda=\rm0.020\,\times50=1.00\,\mathrm{W}$
$\it\Phi_{\rm e}\rm(705)=\it P\rm(705)・\it\Delta\lambda=\rm0.024\,\times50=1.20\,\mathrm{W}$

最後に、いま求まった波長ごとの放射束を足し合わせる▼

　$\it\Phi_{\rm e}\rm(405)+\it\Phi_{\rm e}\rm(455)+\it\Phi_{\rm e}\rm(505)+\it\Phi_{\rm e}\rm(555)+\it\Phi_{\rm e}\rm(605)+\it\Phi_{\rm e}\rm(655)+\it\Phi_{\rm e}\rm(705)$
　$= 0.10 + 0.25 + 0.40 + 0.60 + 0.85 + 1.00 + 1.20$
　$= 4.40\,\mathrm{W}$

これが、白熱電球の波長$380～730\,\mathrm{nm}$の放射束である。

ただし、波長域$50\,\mathrm{nm}$というのは長すぎるため、本当なら$\it\Phi_{\rm e}\rm(\lambda\rm)=\it P\rm(\lambda\rm)\it\Delta\lambda$という式は使えないことにご注意頂きたい。ここでは簡単にするために、あえて長い波長域で話を進めた。正確に求めるのであれば、こちらの分光分布を使わなければならない▼

波長域$2\,\mathrm{nm}$の分光分布であるから、$380～730\,\mathrm{nm}$の波長域を$175$分割している。手計算で$\it\Phi_{\rm e}\rm(\lambda\rm)=\it P\rm(\lambda\rm)\it\Delta\lambda$を$175$回計算するのは無理があるため、ここでは$7$分割とした次第である。

なぜ波長分解するのか

ちなみに、波長域$2\,\mathrm{nm}$の場合で計算すると$4.45\,\mathrm{W}$であり、これが真の値に近い。

ここで質問。

この$4.45\,\mathrm{W}$という値は白熱電球の可視光のパワーを示していると言えるだろうか。

答えは否である。

分光分布が示すのは波長ごとに示された放射量の密度であるから、それらを足し合わせた結果も放射量、すなわち電磁波のパワーである。つまり$4.45$という値は電磁波のパワーであり、可視光のパワーではない。

そもそもなぜ光を波長分解をするのか。放射量を求めるだけなら、（どうせ最後に足し合わせるのだから）波長分解する必要はない。光を波長分解する目的は、放射量を求めることではなく測光量を求めることだ。

なぜ測光量を求めるために波長分解する必要があるのかというと、ヒトの光に対する感じ方は波長ごとに異なるからである。

次稿ではこのあたりの話をしていきたい。